https://www.acmicpc.net/problem/10473
10473번: 인간 대포
입력은 한 개의 길찾기 문제를 표현한다. 첫 줄에는 두 개의 실수가 입력되며 각각은 당신이 현재 위치한 X, Y좌표이다. 두 번째 줄에는 목적지의 X, Y좌표가 실수로 입력된다. 이어지는 줄에는 대
www.acmicpc.net
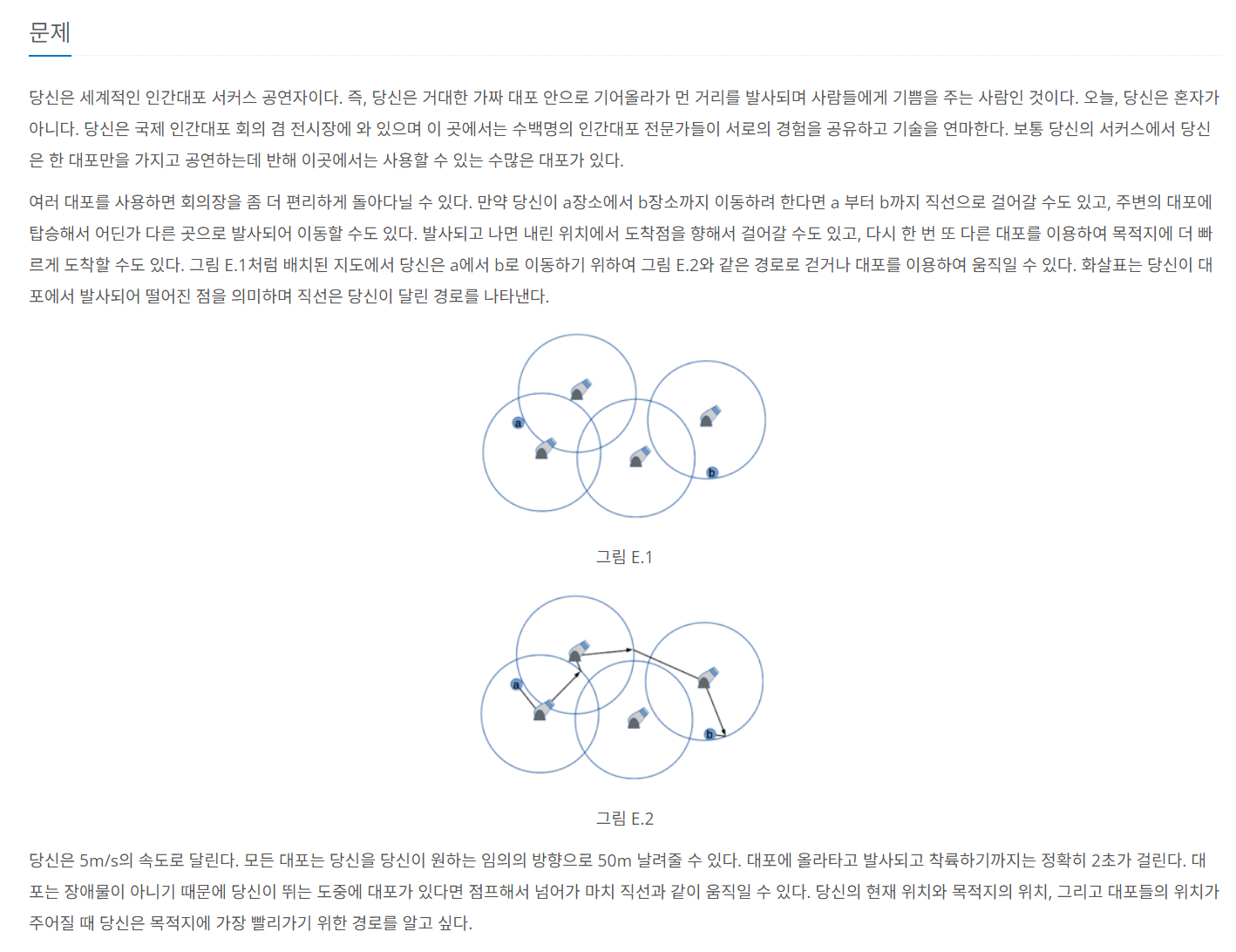

오늘의 문제는 인간 대포이다.
문제를 보자마자, 출발지, 도착지 및 대포들의 위치가 다 해도 100개 언저리기 때문에, 모든 위치들 사이의 거리를 구해서, 얼만큼의 시간이 구하는지를 찾으려고 했다. 이후 다익스트라를 통해 시작점부터 최종 도착 지점까지의 최저 시간을 구하고자 하였다.
import heapq
startx,starty=map(float,input().split())
endx,endy=map(float,input().split())
n=int(input())
data=[]
data.append([startx,starty])
for _ in range(n):
a,b=map(float,input().split())
data.append([a,b])
data.append([endx,endy])
dist=[[1e10 for _ in range(n+2)] for _ in range(n+2) ]
time=[[1e10 for _ in range(n+2)] for _ in range(n+2) ]
q=[[0,0]]
for i in range(1,n+2):
dist[0][i]=((data[i][0]-data[0][0])**2+(data[i][1]-data[0][1])**2)**0.5
time[0][i]=dist[0][i]/5
for i in range(1,n+2):
for j in range(1,n+2):
if i==j:
continue
dist[i][j]=((data[i][0]-data[j][0])**2+(data[i][1]-data[j][1])**2)**0.5
if dist[i][j]<=50:
time[i][j]=min(dist[i][j]/5,(50-dist[i][j])/5+2)
else:
time[i][j]=min(dist[i][j]/5,(dist[i][j]-50)/5+2)
timetables=[1e10 for _ in range(n+2)]
timetables[0]=0
while q:
t,place=heapq.heappop(q)
if timetables[place]<t:
continue
if place==n+1:
print(t)
break
for i in range(n+2):
if place==i:
continue
if t+time[place][i]<timetables[i]:
heapq.heappush(q,[t+time[place][i],i])
timetables[i]=t+time[place][i]
우선, 시작점을 우선적으로 좌표에 저장, 이후 각 대포들을 저장, 마지막으로 도착 지점의 좌표를 저장하였다.
이후, 두 노드까지 걸리는 거리를 저장하는 dist와 걸리는 시간을 저장하는 time을 선언하였다. 이중 for문을 이용하여, dist는 두 점 사이의 거리 공식을 이용하였고, 둘 사이의 거리를 통해, 만약 둘 사이의 거리가 50보다 길 때와, 짧을 때로 if문을 나누었다.
기준이 50 미터인 이유는, 여기서 걸어가게 되면 속도가 5 m/s이다. 대포로는 2초만에 50m를 이동하게 된다. 즉, 거리가 50미터 이하인 경우에는, 5 m/s의 속도로 이동장소까지 걸어서 도달하거나, 대포를 타서, 이후에 걸어가는 것 중 빠른 방법을, 50미터 초과인 경우에는, 대포를 타서 (50미터만큼), 그 남은 거리만큼 걸어가는 것이 최선이다. 그러므로, 케이스를 나눌 수 있었다.
이후 일반적인 다익스트라를 통해, 우리가 원하는 도착장소에 도달하면 걸린 시간의 결과를 출력하였다.
당연하게도, heap을 이용하기 때문에 도착하는 순간이 제일 빨리 도달하는 순간이라고 할 수있다.
'Computer Science > Algorithm' 카테고리의 다른 글
| [Python 3] BOJ 28467: Spell Cards (1) | 2024.02.11 |
|---|---|
| BOJ 17609 회문 [Python 3] (1) | 2024.02.07 |
| [Python 3] BOJ 2243 : 사탕상자 (0) | 2024.01.20 |
| [Python 3] BOJ 30459 현수막 걸기 (0) | 2024.01.19 |
| [Python 3] BOJ 1795 마알 (0) | 2024.01.19 |